Aquantec Ocean provides a flexible risk-analysis framework for the calculation of present values and risk sensitivities under different market-data scenarios and stress tests.

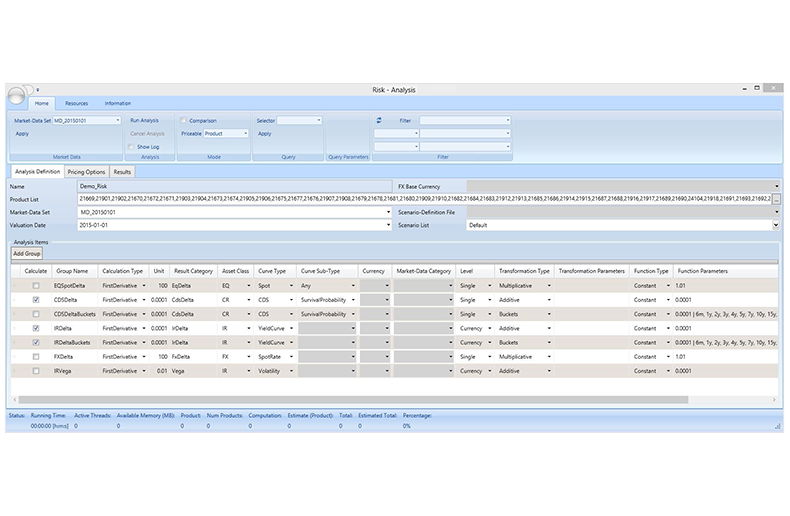
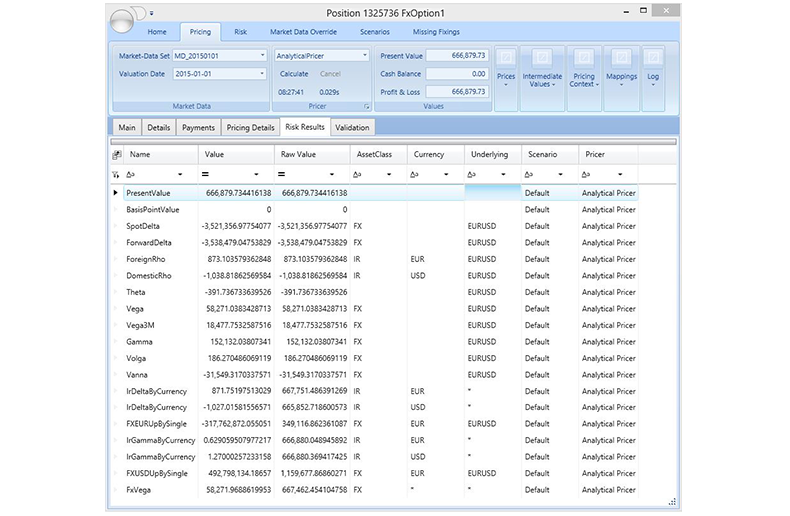
Risk analyses can be performed for selected portfolios and given market-data sets and pricers. A sensitivity analysis may provide risk sensitivities or risk matrices that can be calculated by shifting one or several market-data curves. Greeks such as delta, gamma, and vega can be computed by parallel curve shifts and their bucketed variants by corresponding bucketed shifts. The impact of credit events such as jump-to-default can be evaluated.

The shifts may be applied to a specific curve or to all curves of a specified asset class, curve type, currency, or market-data category. Alternatively, the shifts may be applied to the raw market-data quotes, followed by an automatic curve building.

A what-if analysis may utilize market-data scenarios, which can be defined with a scenario builder by applying sequences of transformations to base market-data sets. Examples for transformations are

• shifting, twisting, and inverting curves,
• riding on the forward curve,
• adding or multiplying polynomial functions,
• appreciation or depreciation of a currency.

Different sub-portfolios can be subjected to different market-data scenarios within a single risk analysis in order to simulate evolving market fragmentations.

The calculations are performed asynchronously and can be executed in parallel on several threads and processors – either locally or distributed with the help of a Calculation Service.